Flood Risk for Power Plant using the Hydraulic Model and Adaptation Strategy
Abstract
This paper provides a mathematical approach for estimating flood risks due to the effects of climate change by developing a one dimensional (1D) hydraulic model for the mountainous river reaches located close to the Yeongwol thermal power plant. Input data for the model, including topographical data and river discharges measured every 10 minutes from July 1st to September 30th, 2013, were imported to a 1D hydraulic model. Climate change scenarios were estimated by referencing the climate change adaptation strategies of the government and historical information about the extreme flood event in 2006. The down stream boundary was determined as the friction slope, which is 0.001. The roughness coefficient of the main channels was determined to be 0.036. The results show the effectiveness of the riverbed widening strategy through the six flooding scenarios to reduce flood depth and flow velocity that impact on the power plant. In addition, the impact of upper Namhan River flow is more significant than Dong River.
Keywords:
1D Hydraulic Model, Thermal Power Plant, Climate Change, Risk Prediction1. INTRODUCTION
Climate change is a global concern because of much more extreme disaster events in the recent year (Anderson and Bau-sch, 2006). One of the key impacts of climate change could be an extreme flood event caused by major storms and heavy rainfall (Bilskie et al., 2016; Easterling et al., 2000). The pro-bability of flood events was estimated to become higher in the future due to climate change (de Bruijn et al., 2017; Jonkman and Vrijling, 2008; Mohleji, 2011; Monirul Qader Mirza, 2002).
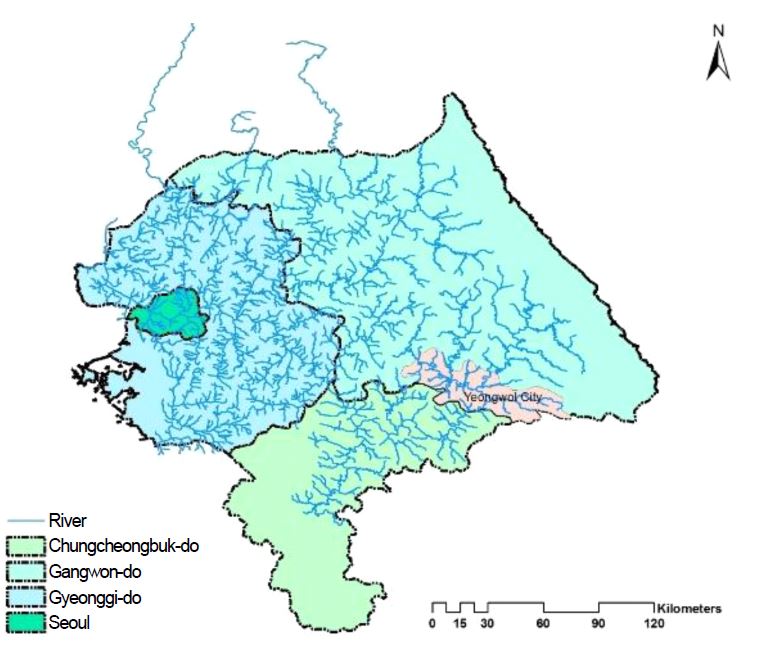
The Han River Basin is located in the North East of South Korea with the high mountain region, the largest basin of the country as well as Korea Peninsula, and is spread over four provinces, including Gangwon-do, Gyeonggi-do, Seoul and Chungcheongbuk-do. The annual average precipitation is app-roximately 1,200 mm during 1961∼1990 (Jeong et al., 2005; Jung et al., 2001), and the rainy season occurs from June to September. Han River Basin can be divided into three sub-basin, including Han, Bukhan and Namhan Sub-basin. Yeong-wol City is located in the East of Namhan Sub-basin (Fig. 1). Under the impact of climate change, the rainy days tend to decrease and the storms become heavier. The heavy rainfall increased from about 100 mm to 222 mm in 1971 and 1980; and, 325 mm in 1992 and 2001 (WWAP, 2009).
Many hydrological models were developed to analyze the climate change impacts on water resources and land use in different basins, including Chungju Basin (Bae et al., 2011) and Hoeya River Basin (Kim et al., 2013). It was found that the trend of water discharges in the river increase in the wet periods and decrease in the dry periods. However, the flood risk prediction in the sub-basin in Yeongwol City was not yet implemented. In Gangwon Province, the rainy season with an extremely high precipitation caused extreme flood event in the summer in 2006 (Chang et al., 2009; Na et al., 2012). Accor-ding to the data collected from Han River Flood Control Office (HRFCO), in the major flood event in July 2006, the peak water level was 11 m in the main channel at Yeongwol Bridge on Dong River.
In this study, a one dimensional hydraulic model was de-veloped for simulating the dynamics of a small reach of Nam-han River and Dong River located in Yeongwol City. Moreover, the flood depths were simulatedby running the model with different scenarios, provided that the upstream urbanarea is protected by full-dyke system.
2. METHODOLOGY
2.1 Model Development
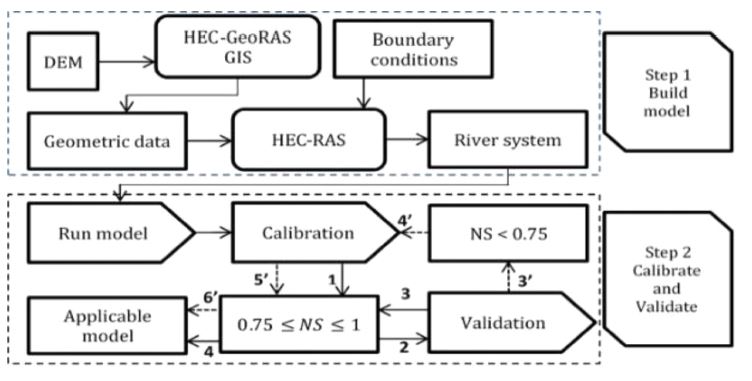
The model was developed in Step 1, and the calibrated and validated in Step 2. The first step includes: (1) obtaining and analyzing the 90 m resolution DEM as map format; (2) con-verting to geometric data by using HEC-GeoRAS tool; and, (3) importing the boundary conditions to HEC-RAS. The model was then calibrated and validated to make sure it was applica-ble (Step 2). In this step, there is 4 main sub-steps including: (1) calculation of Nash-Sutcliffe (NS) values after calibration; (2) validation in a different year; (3) calculation of NS values after validation; and, (4) finishing the model if NS values meet the highest value (0.75≪NS≤1). If NS values are lower than 0.75, there will be 4 extra steps, including: (3’), (4’), (5’) and (6’). Then it is calibrated again until NS meet the highest value (Fig. 2).
This model is a tool for assessing the impact of climate change on the power plant, especially flood events. The applicable model can be used to predict the impacts of climate chan-ge under the future scenarios.
2.2 Model Description
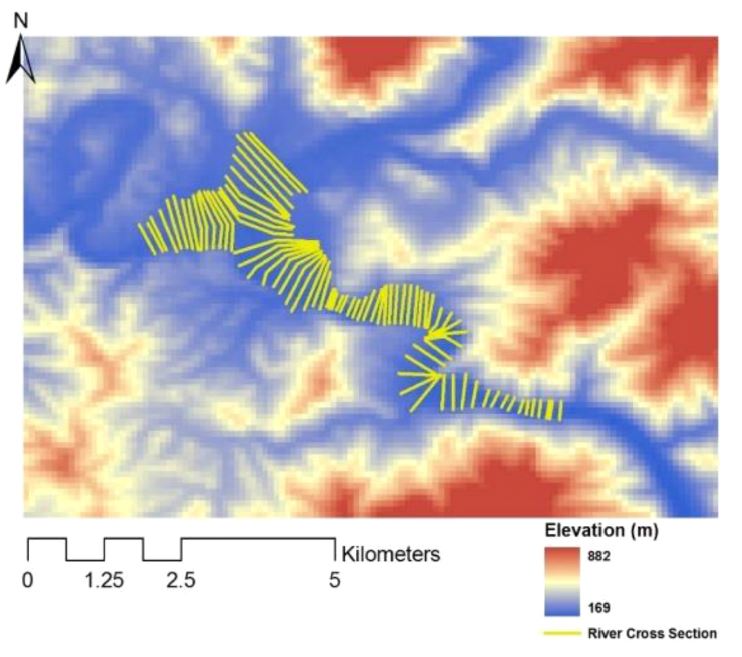
DEM of the study region: The 90 m resolution digital ele-vation model (DEM) was collected from the Consultative Group on International Agriculture Research-Consortium for Spatial Information (available at www.cgiar-csi.org). The DEM of South Korea was obtained to creating geometric data and focused on Yeongwol district, Gangwon Province, which is located near the power plant (Fig. 3). The DEM was used for cross section interpolation, and the cross-sections are then imported to HEC-RAS program to develop the model.
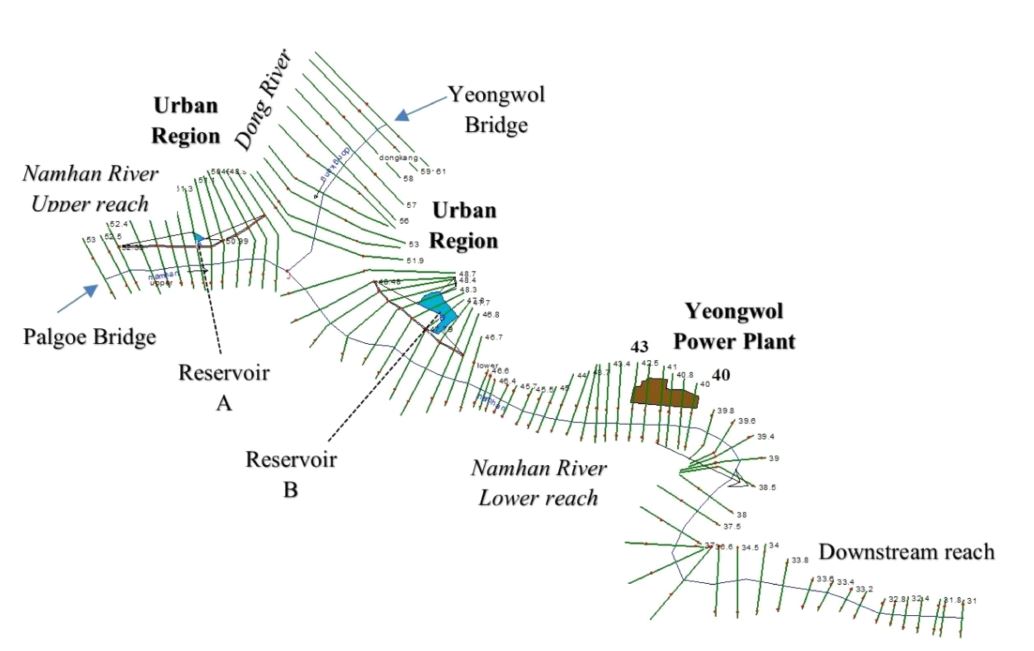
Geometric data: The main geometric data included stream centerlines (the line between two river banks); river cross-sections, created from DEM by using HEC-GeoRAS in combination with GIS program; and, Manning’s n roughness coefficients. The cross-sections were created based on the conditions: (a) the change of channel slopes; (b) the change of river widths; and, (c) the change of curves of the channel. The total length of the Namhan River reach in this study area was approxima-tely 8,000 m (Fig. 4).
Boundary conditions: There are two upstream inputs, inclu-ding flow rates in Yeongwol Bridge, located on Dong River, and Palgoe Bridge, located on Namhan River (Fig. 4). The flow rates (m3·s-1) were measured every 10 minutes and published on HRFCO (availableat www.hrfco.go.kr).
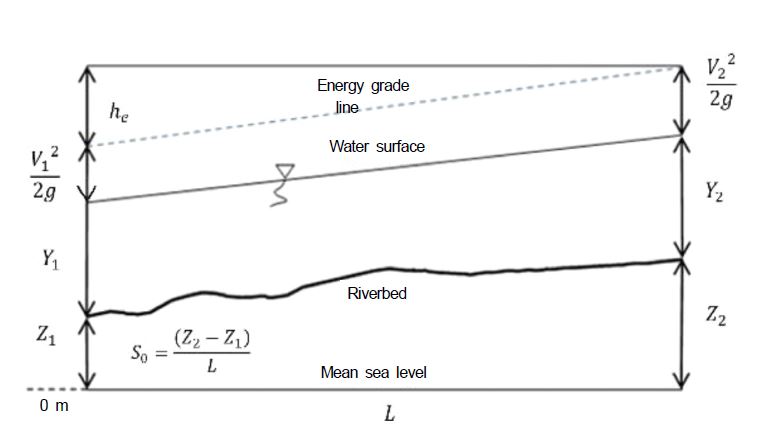
The downstream boundary, which is friction slope, is esti-mated by using the energy equation (Eq. (1)) (Chow et al., 1988) as
| (1) |
where and : elevations of the main channel inverts (m); and : water depths of downstream and upstream (m), respectively; and : average velocities of downstream and upstream (m·s-1),respectively;: gravitational acceleration (m· s-2); and, : energy head loss (m). The representation of terms of energy equation for open channel flow is shown in Fig. 5.
The friction slope (Canestrelli et al., 2014; Cheikh, 2015; Wu et al., 2015) is calculated by Eq. (2).
| (2) |
where : fiction slope; and, : channel length (m).
The friction slope and channel slope have the same value ( = ) in case of unsteady uniform flow (Chow et al., 1988). Applied for the model, the friction slope can be estimated as Eq. (3). Then the value was used as downstream boundary input data.
| (3 ) |
where : channel slope.
In this model, the estimated total length from upstream to downstream reaches is L = 8,000 m. The upstream elevation is = 188 m, and the downstream elevation is = 176 m. Therefore, the friction slope is calculated as = 0.001 and used as the downstream boundary condition.
Manning’s n roughness coefficients is the value indicating the flow obstacle in the rivers. There are many n values depen-ding on different types of channel. The n values are limited between 0.012 and 0.100 for the main channel of natural streams (Alegre et al., 2017; Bilskie et al., 2016; Brunner, 2010; Chow et al., 1988; Savage et al., 2016). Manning’s n equation is important for hydraulic study, it indicates the relation between flow rate, water level, n coefficient and friction slope (Eq. (4) and Eq. (5)).
| (4) |
| (5) |
where : flow rate (m3·s-1); n: Manning’s n roughness coefficient; A: flow area (m2); R: hydraulic radius (m); and, P: wetted perimeter (m).
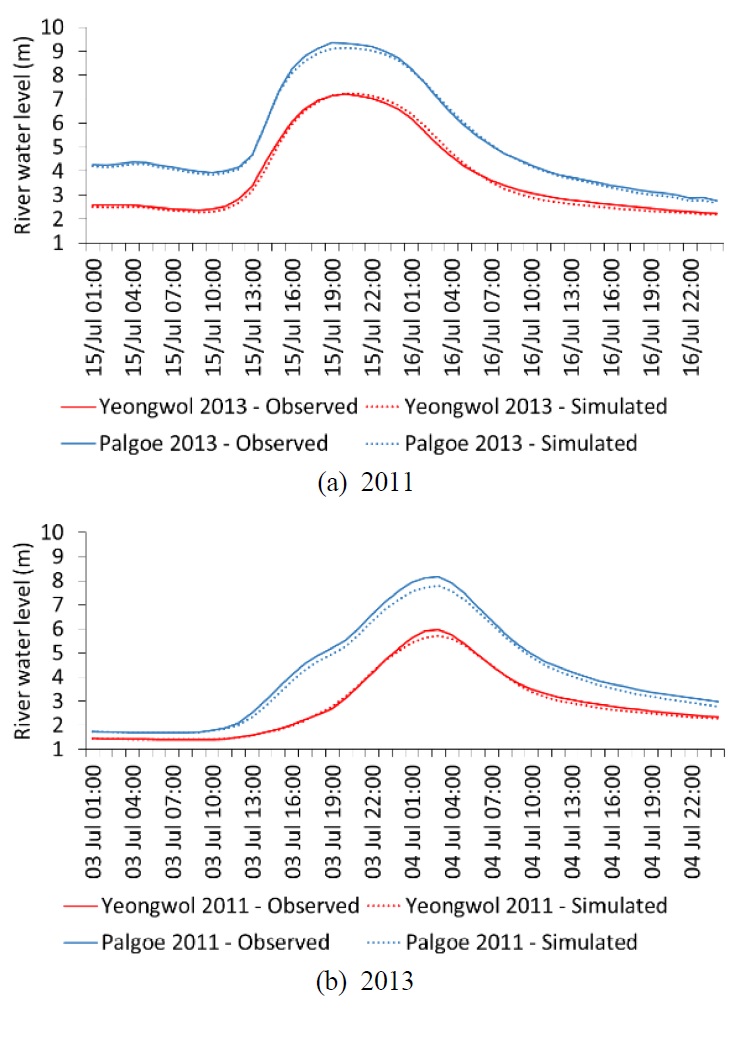
Model running: The year 2013 was chosen for running the model because there was a peak water depth of the period bet-ween 2009 and 2014, and the data of two upstream boundary conditions are sufficient. At Yeongwol Bridge Station, the maxi-mum water level is 7.14 m on July 15th, and the maximum flow rate is approximately 7,000 m3·s-1. At Palgoe Bridge Station, the maximum water level is 9.40 m, and the maxi-mum flow rate was nearly 5,700 m3·s-1.
2.3 Calibration and Validation
J. E. Nash and J.V. Sutcliffe created one index called Nash-Sutcliffe index (NS) that represents the accuracy of hydrolo-gical and hydraulic models (Habert et al., 2016; Nash and Sut-cliffe, 1970). Harmel et al. (2010) developed a watershed model was calibrated by using NS index, and it shows that the NS values are greater than 0.90 resulting in a good applied model (0.75≪NS≤1) (Moriasi and Arnold, 2007). The NS index was also used to calibrate the hydraulic model. For example, Panda et al. (2010) and Paiva et al. (2011) used NS to calibrate the hydraulic model for river networks. Besides, there were vari-ous studies using NS for comparing the simulated and observed water levels and discharge in 1D hydraulic model recently (de Paes and Brandão, 2013; Lotsari et al., 2014; Meert et al., 2016; Saleh et al., 2013).
The NS value is calculated in Eq. (6). If the NS closes to one (100%), the model will be acceptable and can be applied.
| (6) |
where NS: Nash-Sutcliffe Index; : simulated value at the time i; : observed value at the time i; : average observed value in the period of calibration; m: number of hours.
In this case, X value represents the water level of the channel. Therefore, , , and were simulated, observed, and average observed water levels, respectively. In addition, the output data was simulated hourly and decided as 2,208 hours, from July 1st to September 30th, and that means m = 2,208.
The Manning’s n roughness coefficients of the main channel were adjusted to make the simulated water levels closed to observed values. The model was tested with different n coeffi-cients in a range from 0.012 to 0.100, and it would be stopped if the NS index met the highest values.
After calibration, the model was validated by running in the different periods, i.e. 2011, 2012 and 2014, to make sure that it is reasonable for other years. If the NS values were much lower than one, the n values would be adjusted again until it was applicable. The model was then computed in the first period, i.e. the year 2013, to make it applicable (Fig. 2).
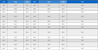
Table 1 shows the Nash-Sutcliffe index of two upstream stations under calibration and validation. The results indicated that the NS values were very high, and it can be apply for simulation and prediction. Moreover, it was found that the Manning’s n coefficient in the main channel of Namhan River and Dong River was 0.036, and it was used for all river cross sections.
The comparisons of water levels in the two upstream stations are shown in Fig. 6(a) and Fig. 6(b), and explained for the accu-racy of the model (NS index). The periods of the highest water level was chosen to compare. The peak water level usually occurred in the period from 2nd to 16th of July in 2011 and 2013. Moreover, the simulated water levels almost equal to the observed values. The maximum water levels in 2012 and 2014 were quite low compared to the other years. The maximum observed and simulated water levels were 3.57 m and 3.54 m in 2012; and 2.47 m and 2.34 m in 2014, respectively.
2.4 Future Scenarios
The comparison of the discharges shows that the flood events in 2006 and the highest water level in 2013 occurred in the same period, i.e. the period from July 15th to July 17th, at Yeongwol Bridge Station. The scenarios were determined based on the extreme flood event in 2006 and strategies to resist these problems. The maximum discharge in 2006 (about 19,000 m3·s-1) was approximately three times greater than that in 2013, which was nearly 6,000 m3·s-1.
The data of discharges and water levels at Yeongwol Bridge Station in 2006 is sufficient; however, the hydrodynamic data at Palgoe Bridge station in 2006 is missing. It was assumed that the future discharges at Yeongwol Bridge Station are three times greater than the flow in 2013 (Extremely High Flow). In addition, it was assumed that there will be three conditions for Palgoe Bridge Station in the future including: (1) the future flow equals to the flow in 2013 (Low Flow); (2) the future flow is double the flow in 2013 (High Flow); and, (3) the future flow is triple the flow in 2013 (Extremely High Flow). According to the data collected from HRFCO, a riverbed expansion strategy was decided in order to prevent the impact of flood event. The cross sections of the rivers were expanded to the maximum width and depth but the stable flow was still ensured. In this case, the average expanded depth is approximately 4 m, such as cross sections 48.7 and 31 [Fig. 4, Fig. 7(a) and 7(b)].
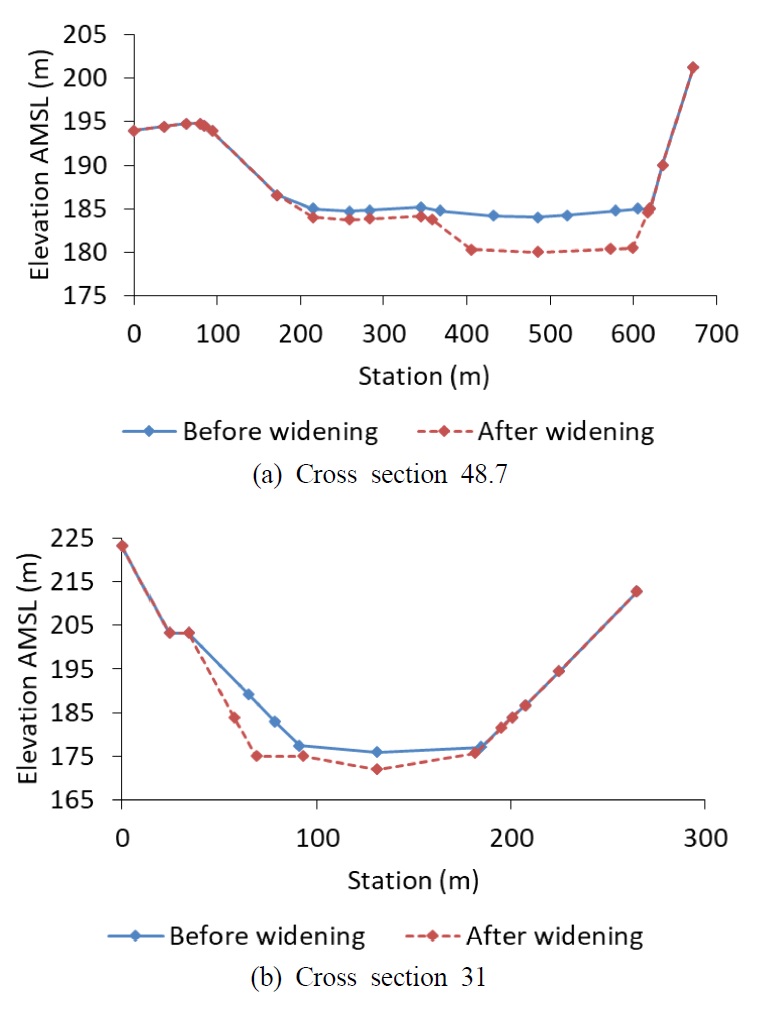
Cross section data before and after widening at the upstream and downstream of the lower reach of Namhan River (AMSL: above mean sea level).
There are six scenarios based on the combination between future climate change conditions and the adaptation strategy (Table 2).
3. RESULTS AND DISCUSSION
3.1 Water Surface Elevations
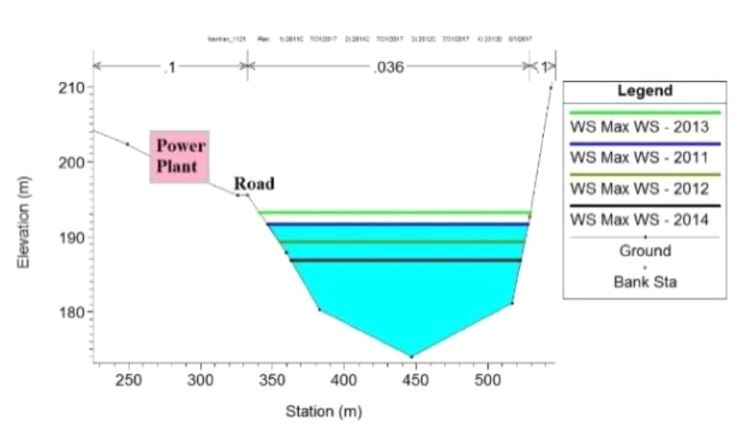
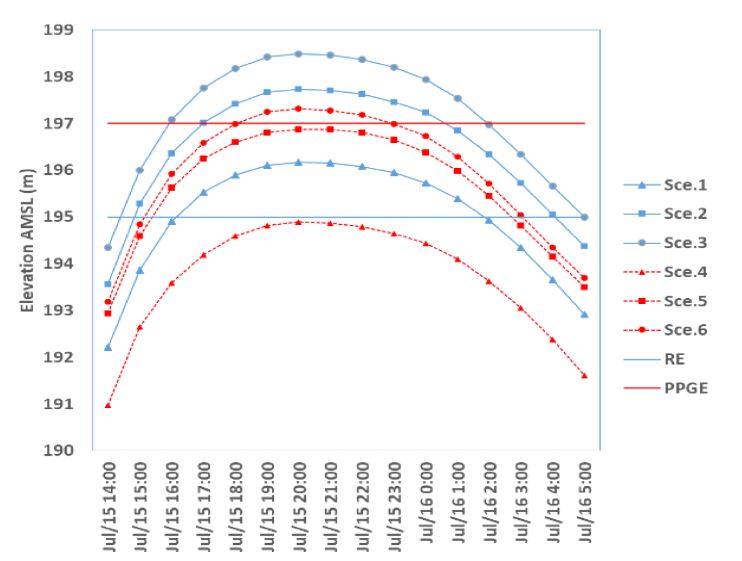
According to the survey, the minimum ground surface ele-vation of the power plant is approximately 197 m, two-meter higher than the elevation of the road elevation (195 m). The cross section 42.5, located near the power plant, was chosen to analyze. Fig. 8 shows the simulated maximum water sur-face elevations from 2011 to 2014. The lowest elevation is in 2014 (black line) and the highest is in 2013 (yellow line). The historical maximum water elevations are below the bank sta-tion (road). The highest elevation in 2013 is approximately 193.3 m, and the lowest elevation in 2014 is 186.9 m. The depths in 2011 and 2012 are 191.7 m and 189.3 m, respectively. The maximum velocity is ranged from 1.8 m·s-1 (2014) to 3.4 m·s-1 (2013).
The results shows that the maximum water surface eleva-tion (Max WSE) of Sce. 3 is extremely higher than the power plant ground elevation (PPGE). After widening the riverbed, Max WSE Sce. 6 is slightly greater than the PPGE. The flood depths under most of scenarios are extremely high compared to the road elevation (RE) except Sce. 4 (Fig. 9). Although the water flow of Dong River is extremely high, the risk will be low if the flow of the upper Namhan River is low (Sce. 4). Other scenarios shows that the extremely high water flows in both upper reaches (i.e. upper Namhan and Dong River) can cause the flood. Therefore, the higher flow of the upper Nam-han River affects the downstream reach more significantly than Dong River.
The flood depths under Sce. 1, Sce. 4 and Sce. 5 do not affect the power plant. Sce. 2 and Sce. 3 affect the power plant with the maximum depth are 0.43 m and 1.52 m above the PPGE respectively. Despite widening the riverbed, Sce. 6 still impacts on the PPGE with the maximum depth is 0.34m (Fig. 9 and Table 3).
In the comparison between Sce. 1 and Sce. 4, only flood depths under Sce. 1 affects the RE. Therefore, the riverbed wi-dening strategy is highly effective for this case (low flow of the upper Namhan River). For the second case (high flow of the upper Namhan River), the widening strategy is useful for preventing the flood impact on the PPGE, with the maximum flood depth decreases from 0.43 m in Sce. 2 to 0.00 m in Sce. 5; however, it is not effective for the RE. The widening stra-tegy may reduce the flood depths but may not be helpful for both PPGE and RE in the third case (extremely high flow of the upper Namhan River).
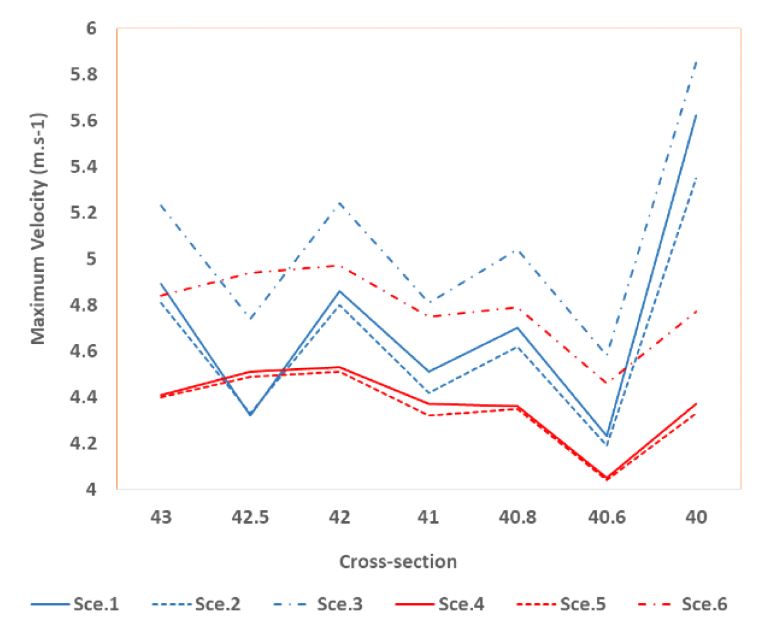
3.2 Velocities
A small part of lower Namhan River, from cross-section 43 to cross-section 40, was chosen to compare the velocities among the scenarios. It can be seen that the maximum velocities of the river will decrease if the riverbed is widened. The velocity under Sce. 4 is lower than Sce. 1; the velocity under Sce. 5 is lower than Sce. 2; and, velocity under Sce. 6 is lower than Sce. 3 (Fig. 10). The very high velocities cause river bank ero-sion, the riverbed widening strategy therefore help to reduce the risk of bank erosion.
4. CONCLUSIONS
In this research, the historical and topographical data are used for developing the one dimensional hydraulic model for predicting the water levels based on the climate change sce-narios. The accuracy of the model is very reliable with the NS values, are more than 0.9 through calibration and validation, result in the model can be applied for studying the climate change prediction.
The flood depths will decrease significantly if the riverbed is widened. The expected scenario is Sce. 4 and the most ex-treme flood event scenario is Sce. 3. The riverbed widening is an effective strategy for flood prevention for both road and power plant in the case that the water flow of Dong River is extremely high and the flow of the upper Namhan River is low. In case of high flow of the upper Namhan, the strategy is only effective for the power plant, and it is not effective for both power plant and road in case of the extremely high flow case. Besides, riverbed widening can help reduce the wa-ter velocities and therefore decrease the risk of bank erosion. Although the flow of Dong River is high, the risk will be not significant if the flow of the upper Namhan River is low under the widening strategy. Therefore, the impact of high flow of the upper Namhan River is more important than Dong River.
Although the results can help evaluate and predict the flood risk depending on future climate change scenarios, there remain some limitations. The riverbed elevations were just interpolated from the digital elevation model with the low resolution. In the further study, the two dimensional models with lateral structures should be developed. Moreover, the hydrological model with the relation between rainfall, basin and discharge should be studied.
Acknowledgments
This project is supported by the “R&D Center for reduction of Non-CO2 Greenhouse gases (2016001690005)” funded by Korea Ministry of Environment (MOE) as “Global Top Envi-ronment R&D Program”.
References
- Alegre, P., Ferreira, DM., Gomes, J., (2017), Verification of Saint-Venant equations solution based on the lax diffusive method for flow routing in natural channels, Brazilian J. Water Resour.
- Anderson, J., Bausch, C., (2006), Climate change and natural disasters: Scientific evidence of a possible relation between recent natural disasters and climate change.
-
Bae, DH., Jung, IW., Lettenmaier, DP., (2011), Hydrologic uncertainties in climate change from IPCC AR4 GCM simulations of the Chungju Basin, Korea, J Hydrol, 401, p90-105.
[https://doi.org/10.1016/j.jhydrol.2011.02.012]

- Bilskie, MV., Hagen, SC., Alizad, K., Medeiros, SC., Passeri, DL., Needham, HF., Cox, A., (2016), Dynamic simulation and numerical analysis of hurricane storm surge under sea level rise with geomorphologic changes along the northern Gulf of Mexico, Earth’s Futur, pn/a-n/a.
- Brunner, G., (2010), HEC River Analysis System (HEC-RAS), http://www.hec.usace.army.mil/.
-
Canestrelli, A., Lanzoni, S., Fagherazzi, S., (2014), One-dimensional numerical modeling of the long-term morphodynamic evolution of a tidally-dominated estuary: The lower fly river (Papua New Guinea), Sediment Geol, 301, p107-119.
[https://doi.org/10.1016/j.sedgeo.2013.06.009]

-
Chang, H., Franczyk, J., Kim, C., (2009), What is responsible for increasing flood risks? The case of Gangwon Province, Korea, Nat Hazards, 48, p339-354.
[https://doi.org/10.1007/s11069-008-9266-y]

- Cheikh, MB., 2015. Using of Hec-ras model for hydraulic analysis of a river with agricultural vocation: A case study of the Kayanga river basin, Senegal, American Journal of Water Resources, 3(5), p147-154.
- Chow, VT., Maidment, DR., Mays, LW., (1988), Applied hydrology, McGraw-Hill.
-
de Bruijn, K., Buurman, J., Mens, M., Dahm, R., Klijn, F., (2017), Resilience in practice: Five principles to enable societies to cope with extreme weather events, Environ Sci Policy, 70, p21-30.
[https://doi.org/10.1016/j.envsci.2017.02.001]

-
de Paes, RP., Brandão, JLB., (2013), Flood control in the Cuiab? River Basin, Brazil, with multipurpose reservoir operation, Water Resour Manag, 27, p3929-3944.
[https://doi.org/10.1007/s11269-013-0388-y]

-
Easterling, DR., Meehl, GA., Parmesan, C., Changnon, SA., Karl, TR., Mearns, LO., (2000), Climate extremes: Observations, modelling, and impacts, Science, 289, p2068-2074.
[https://doi.org/10.1126/science.289.5487.2068]

-
Habert, J., Ricci, S., Le Pape, E., Thual, O., Piacentini, A., Goutal, N., Jonville, G., Rochoux, M., (2016), Reduction of the uncertainties in the water level-discharge relation of a 1D hydraulic model in the context of operational flood forecasting, J Hydrol, 532, p52-64.
[https://doi.org/10.1016/j.jhydrol.2015.11.023]

- Harmel, RD., Smith, PK., Migliaccio, KW., (2010), Modifying goodness-of-fit indicators to incorporate both measurement and model uncertainty in model calibration and validation, Trans ASABE, 53, p55-63.
- Jeong, CS., Heo, JH., Bae, DH., Georgakakos, KP., (2005), Utility of high-resolution climate model simulations for water resources prediction over the Korean peninsula: A sensitivity study, Hydrol Sci Journal-Journal Des Sci Hydrol, 50, p139-153.
-
Jonkman, SN., Vrijling, JK., (2008), Loss of life due to floods, J Flood Risk Manag, 1, p43-56.
[https://doi.org/10.1111/j.1753-318x.2008.00006.x]

-
Jung, HS., Lim, GH., Oh, JH., (2001), Interpretation of the transient variations in the time series of precipitation amounts in Seoul, Korea. Part I: Diurnal variation, J Clim, 14:, p2989-3004.
[https://doi.org/10.1175/1520-0442(2001)014<2989:iottvi>2.0.co;2]

- Kim, J., Choi, J., Choi, C., Park, S., (2013), Impacts of changes in climate and land use/land cover under IPCC RCP scenarios on streamflow in the Hoeya River Basin, Korea, Sci Total Environ, p452-453, 181-195.
-
Lotsari, E., Aaltonen, J., Veijalainen, N., Alho, P., Käyhkö, J., (2014), Future fluvial erosion and sedimentation potential of cohesive sediments in a coastal river reach of SW Finland, Hydrol Process, 28, p6016-6037.
[https://doi.org/10.1002/hyp.10080]

-
Meert, P., Pereira, F., Willems, P., (2016), Computationally efficient modelling of tidal rivers using conceptual reservoirtype models, Environ Model Softw, 77, p19-31.
[https://doi.org/10.1016/j.envsoft.2015.11.010]

- Mohleji, S., (2011), Gaining from losses: Using disaster loss data as a tool for appraising natural disaster policy, Pro-Quest Diss Theses.
-
Monirul Qader Mirza, M., (2002), Global warming and changes in the probability of occurrence of floods in Bangladesh and implications, Glob Environ Chang, 12, p127-138.
[https://doi.org/10.1016/s0959-3780(02)00002-x]

- Moriasi, D., Arnold, J., (2007), Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, Transactions of the ASABE, 50, p885-900.
- Na, JI., Okada, N., Fang, L., (2012), Utilization of the Yonmenkaigi system method for community building of a disaster damaged village in Korea, Conf Proc IEEE Int Conf Syst Man Cybern, p3093-3098.
- Nash, JE., Sutcliffe, JV., (1970), River flow forecasting through conceptual models, J Hydrol, 10, p282-290.
-
Paiva, RCD., Collischonn, W., Tucci, CEM., (2011), Large scale hydrologic and hydrodynamic modeling using limited data and a GIS based approach, J Hydrol, 406, p170-181.
[https://doi.org/10.1016/j.jhydrol.2011.06.007]

-
Panda, RK., Pramanik, N., Bala, B., (2010), Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model, Comput Geosci, 36, p735-745.
[https://doi.org/10.1016/j.cageo.2009.07.012]

-
Saleh, F., Ducharne, A., Flipo, N., Oudin, L., Ledoux, E., (2013), Impact of river bed morphology on discharge and water levels simulated by a 1D Saint-Venant hydraulic model at regional scale, J Hydrol, 476, p169-177.
[https://doi.org/10.1016/j.jhydrol.2012.10.027]

-
Savage, JTS., Bates, P., Freer, J., Neal, J., Aronica, G., (2016), When does spatial resolution become spurious in probabilistic flood inundation predictions?, Hydrol Process, 30, p2014-2032.
[https://doi.org/10.1002/hyp.10749]

- Wu, T., Zheng, Z., Ma, W., (2015), Application of HEC-RAS in floating bridge calculation of the backwater height, p205-208.
- WWAP, (2009), The United Nations world water development report 3, Case study volume: Facing the challenges, World water.