Spatial impacts of digital industry development on carbon emission intensity: Empirical evidence from China
Abstract
The digital industry, as a new driver for high-quality economic development, is poised to play a pivotal role in energy conservation and carbon reduction in the era of climate change. This study explores the relationship between the digital industry's growth and carbon emission intensity, including empirical testing of this relationship. We also examine whether regional industrial and socio-economic factors in China induce spatial spillover effects on carbon emissions. To this end, we employ a Spatial Durbin Model (SDM) with fixed effects to analyze provincial-level panel data from 2005 to 2019. The empirical findings suggest that China's digital sector's progress can potentially lower carbon emission intensity. However, this reduction effect varies regionally, being more pronounced in the central and eastern regions than in the less developed western regions. When contemplated through a spatial lens, the digital industry's evolution appears to contribute to localized and broader carbon emission reductions. Yet, our study indicates that the spatial spillover effect among provinces remains limited. In addition, our research identifies a significant inverse relationship between economic development and carbon emission intensity, suggesting that economic growth may lead to reduced emissions. On the other hand, a larger labor force, aging population, foreign trade are positively correlated with higher emissions. Controlling for the level of digital industry development and industrial structure, R&D investment is found to be associated with higher emission intensity. This paper not only offers a novel understanding of the digital industry's impact on carbon emissions but also provides policy insights for integrating environmental sustainability into China's economic and social development towards carbon neutrality.
Keywords:
Carbon Neutrality, Carbon Emission Intensity, Green Growth, Digital industrialization, Spatial Autocorrelation, Spatial Durbin Model.1. Introduction
Global warming, driven primarily by rising carbon emissions, poses a significant threat to human habitats and food security due to its potential to cause frequent droughts, glacial melt, rising sea levels, and extreme weather events. According to BP's Statistical Review of World Energy (BP, 2023), China has been the world's largest carbon emitter since 2005, surpassing the United States. Despite a brief decline in 2020, global carbon emissions are on the rise again.
In response, the international community has initiated collective actions to combat carbon emissions and promote sustainable development. Key initiatives include the 1997 Kyoto Protocol, which imposed legal obligations to reduce emissions on developed countries following the principle of common but differentiated responsibilities, and the 2015 Paris Agreement, aiming to limit global temperature increases to 2°C above pre-industrial levels, with an ideal target of below 1.5°C. China, as a major emitter, primarily produces carbon through fossil fuel use in industrialization. The country's ineffective development strategies and poor industrial planning have exacerbated this issue. However, at the 2020 United Nations General Assembly, China committed to peaking carbon emissions by 2030 and achieving carbon neutrality by 2060. Subsequent measures include the implementation of a carbon emissions trading pilot in 2013 and a national trading market in July 2021, initially focusing on power generation. In August 2022, Chinese agencies released a plan for technological innovations to support these goals, emphasizing green technology research and development.1)
Furthermore, amidst the information revolution, China's digital industry is experiencing rapid expansion. Inter-regional cooperation is steadily growing stronger. The China Digital Economy Development Report (CDEDR, 2023) showed that the digital economy reached 50.2 trillion yuan in 2022, accounting for 41.5% of the national GDP. The report outlines that the digital economy consists of four key components: digital industrialization, industrial digitalization, digital governance, and data valuation. Among these components, the software and information technology services sector, a high-value-added tertiary industry, is a crucial part of digital industrialization. This growth, along with the emergence of new business models, is reshaping industrial structures. Digital technologies also present opportunities for reducing carbon emissions, making it crucial to understand the relationship between digital industrialization and emissions for achieving China's carbon goals.
To this end, our study examines the impact of the digital economy on carbon emission intensity, with a particular focus on the impact of digital industrialization on regional carbon emissions in China and the potential spatial correlations between these regions. It also aims to provide insights to help China achieve its strategic goals of reaching the "carbon peak" and "carbon neutrality", while promoting low-carbon digital industrialization. The paper is organized as follows: Section 2 reviews the previous literature, Section 3 describes the research methods and data, Section 4 presents the empirical findings, and Section 5 concludes the study.
2. Literature review
The rapid expansion of industrial scale and extensive use of fossil fuels have led to significant environmental issues, notably the emission of greenhouse gases like carbon dioxide. Research on carbon emissions falls into two categories: studies focusing on measuring and analyzing emissions across regions and sectors, and those discussing the factors influencing emissions. Understanding these factors is crucial for managing carbon reduction efforts. Literature reviews show that scholars use methods like index decomposition and econometric modeling to assess the impact of economic scale, technological innovation, population, industrial structure, and energy consumption on carbon emissions. Demographic aspects, especially urbanization and population size, have been significant in previous studies.
Liu et al. (2011) found that population growth and urbanization increase indirect carbon emissions. Dong et al. (2016) used spatial econometrics and dynamic panel co-integration method to analyze the impact of urbanization and energy composition on China's carbon emission intensity (CEI), finding both factors help mitigate CEI. Zhou et al. (2021) observed that population density encourages technological abatement strategies, while Ali et al. (2019) noted urbanization's negative environmental impact in Pakistan. Hwang et al. (2021) employed the Invest carbon model to evaluate the impact of urban land use on carbon storage in Korean urban areas, finding that urbanization reduces areas functioning as carbon sinks. In addition, Studies consistently show that economic growth leads to increased carbon emissions and energy consumption (Guo et al., 2016; Ali et al., 2017; Luo et al., 2023). The Environmental Kuznets Curve (EKC) hypothesis, suggesting an inverted U-shape relationship between environmental quality and economic growth, has been a focus of research.
More recently, technological innovation, energy utilization, and industrial development have become key areas of research regarding their impact on carbon emission intensity. Huang et al. (2018) showed that increased R&D expenditure leads to reduced carbon emission intensity, based on their analysis of data from 30 Chinese regions. Cheng et al. (2018) found that both industrial structure and technological innovation affect carbon emission intensity, with the latter playing a more significant role. Zhang et al. (2017) highlighted the critical role of environmental innovation, especially technological innovation and energy efficiency, in reducing carbon emission emissions in China. In addition, Kim et al. (2019) analyzed greenhouse gas emission efficiency (GEE) to assess emission reduction policies in Korea. Findings indicated industry-wide efficiency gains in 2011 ~ 2012, a subsequent decline, and a rebound with the introduction of an emission trading scheme. Adedoyin et al. (2020) used the fully modified ordinary least square (FMOLS) and dynamic ordinary least square (DOLS) techniques to analyze the impact of economic growth and R&D in 16 European Union countries, finding that R&D adversely impacts carbon emissions. Ki and Seong (2023) noted that despite advances in technology for carbon emission reduction, significant mitigation has not yet been achieved.
In the digital industry, there are various hypotheses about its potential impact on carbon emissions, focusing on digital technological innovation and industrial structure. The digital industry, based on digitized knowledge and information, can shift from traditional resource-intensive models to sustainable, high-quality growth. Xie (2022) states that the digital industry, including telecommunications and IT services, is more environmentally friendly than traditional industries. Li and Sun (2022) found that the information and communication industry achieves carbon reduction by substituting clean energy for coal-based electricity, optimizing electricity supply and demand, and improving production efficiency.
However, some studies suggest the digital industry might increase carbon emissions. Ge et al. (2022) argue that despite focusing on R&D and human capital, the digital industry still consumes energy in producing electronic components and machinery, leading to increased carbon emissions. Jiang (2021) used data from 277 Chinese cities to show that the digital economy and carbon emissions follow the Environmental Kuznets Curve (EKC), with a significant accumulation of carbon dioxide during the phase of digital industrialization.
Despite extensive research on carbon emissions, the complex relationships between carbon emission intensity and its drivers remain unclear. In addition, the academic community lacks consensus regarding on the impact of the digital economy on carbon emissions, which varies according to the definitions and contexts. Moreover, empirical research on the potential spatial spillover effects of the digital economy across China's regions is scarce. To address these gaps, this study applies spatial econometric methods to examine how China's digital industry development affects carbon emission intensity. This research aims not only to deepen understanding of the role of the digital industry development in carbon emissions but also to provide a basis for policies that promote sustainable development and carbon neutrality.
3. Methodologies and data definitions
3.1. Methodologies
The STIRPAT (Stochastic Impact by Regression on Population, Affluence, and Technology) model is pivotal for examining the disproportionate effects of human activities on the environment. Its ability to incorporate additional variables beyond population, affluence, and technology is a key aspect. This feature allows for a thorough analysis of environmental impacts, highlighted by Anser (2019). Our study explores the complex relationship between the digital industry development and carbon emissions using a two-way fixed effects model that accounts for both provincial and temporal variations. To evaluate its applicability in this study, we use the Hausman test in our empirical analysis. The model is defined as follows:
| (1) |
In this framework, the variables of the model are defined as: i for the provinces, and t for the years in the dataset. CEIit indicates the level of carbon emission intensity. DIGITALit measures the development of the digital industry2). Xit consists of control variables affecting carbon emissions. μi represents provincial fixed effects, reflecting time-invariant unique provincial traits. λi denotes time-fixed effects that control for changes over time. ϵit captures the model's random disturbances. β0 is the intercept term. β1 is the coefficient that quantifies the impact of the digital industry development on carbon emission intensity, where βk for k = 2, ..., n indicates the coefficients associated with the control variables' influence on the carbon emission intensity.
Spatial weight matrices are critical in spatial analysis, particularly for carbon emissions studies. They generally include: 1. Adjacency Matrix. This assesses geographical adjacency, implying spatial correlation. However, in carbon emissions research, the correlation may extend beyond mere proximity. 2. Distance Matrix. It measures spatial relationships based on physical distance, suggesting closer units are more connected. This can miss other relevant factors in carbon emissions. 3. Nested Matrix. This advanced type integrates multiple proximity levels and various factors influencing spatial relationships. Addressing the shortcomings of traditional adjacency-based matrices, our study following Zhang and Hu (2020), introduces a geographic-economic nested matrix Eq. (2). This novel approach combines geographical distances with economic interdependencies, enhancing the analysis of spatial correlations in carbon emissions. The geographic-economic nested matrix captures the intricate interplay of proximity and economic connections, providing a richer analytical tool for this field.
| (2) |
Where dij refers to the actual geographical distance between the centroids of two regions. β defaults to 1, and PGDPi represents the average per capita GDP of region i during the study period, and PGDPj represents the average per capita GDP of region j during the same period. e indicates the natural constant. The geographic-economic nesting matrix is used in this paper to account for the fact that closer geographical proximity between regions implies stronger interdependence and correlation of socio-economic activities, while greater geographical distance diminishes such correlation. This matrix is standardized for model computation, ensuring it appropriately scales spatial relationships.
This study employs the Spatial Durbin Model (SDM) for its spatial econometric analysis because of its flexibility and comprehensive ability to capture spatial dependencies. Unlike the Spatial Lag Model or the Spatial Error Model, the SDM takes into account both the spatial lag of the dependent and independent variables, allowing it to comprehensively assess the impact of neighboring units' variables on a local unit. Furthermore, the SDM distinguishes between direct (local) effects and indirect (spillover) effects of explanatory variables, which is crucial for understanding regional interdependencies (Golgher and Voss, 2016). Recognizing the inherent advantages of the SDM, this research initially opts for its adoption as the foundational model for empirical analysis. Subsequently, it subjects the model to rigorous spatial adequacy tests, thereby ascertaining its appropriateness as the optimal model for the investigation. As a result, this study introduces key components into the SDM framework, including carbon emission intensity, spatial lag terms for carbon emission intensity, and spatial lag terms for explanatory variables, thereby formulating the following SDM for comprehensive analysis and assessment.
| (3) |
In Eq. (3), the components are defined as follows: CEIit stands for carbon emission intensity and is the dependent variable in the model. ρ is the spatial lag coefficient, which indicates the degree of spatial autocorrelation of the dependent variable. Wij is an element of the spatial weight matrix W, representing the spatial relationship between units i and j. β0 is the intercept. Xikt is the observation of the kth independent variable for spatial unit i at time t, indicating the level of digital industry development.The model also includes a range of control variables, in line with established research methodologies. βk are the coefficients for the direct effects of the independent variables Xk. γk are the coefficients for the spatial lag of the independent variables, reflecting the indirect (spillover) effects of Xk in neighboring units on CEIit.Furthermore, ui is the individual fixed effect and λt is the time fixed effect. ϵit is the error term.
Indeed, considering the geographical unit measurement of carbon emission intensity levels in China, it is crucial to perform a spatial autocorrelation analysis to gauge the spatial dependence of these levels before advancing to the SDM for in-depth investigation. The global Moran's I index (Moran, 1950) is a valuable tool for this purpose, and it can be expressed as follows:
| (4-1) |
| (4-2) |
Eq. (4-1) is defined as follows: I is the Moran's I index, measuring spatial autocorrelation where n=28.3) CEIi and CEIj represent the observations for regions i and j, respectively, specifically denoting the carbon emission intensity of different provinces in China. represents the mean of the observations. Wij stands for the spatial weight matrix, specifically indicating the geographic-economic nested matrix. To ascertain the presence of spatial autocorrelation in the observations, a statistical measure Z is utilized to evaluate the significance level of Moran's I index, as shown in Eq. (4-2). E(I) represents the expected value of the Moran's I index. Var(I) represents the variance of the Moran's I index. When |Z(I)| ≥ 1.96, it is considered that carbon emission intensity exhibits spatial autocorrelation at a 5% significance level.
The global Moran's I index is used to analyze the overall spatial variation in carbon emission intensity and does not elucidate local spatial clustering strength. This study will employ the local Moran's I index method to analyze the spatial dependence of carbon emission intensity between provinces and neighboring provinces. Additionally, a Moran's I index scatter plot will be used to observe significant clustering categories within provinces, as expressed by Eq. (5).
| (5) |
In Eq. (5), I' represents the Local Moran's I index, which is a local measure of spatial autocorrelation. The meanings of the other indicators are consistent with those explained in Eq. (4).
3.2. Data definitions
This study examines a dataset covering 30 provinces and regions in China from 2005 to 2019. The main objective is to analyze the intricate relationship between carbon emission intensity and the digital industry development in these areas. Our empirical model incorporates key factors known to influence carbon emission intensity based on previous studies. Table 1 provides a detailed overview of the determinants considered in this analysis.
Data for the explanatory variables are obtained from the National Bureau of Statistics of China (NBS, 2023), while information on total carbon emissions are from the Carbon Emission Accounts and Datasets for Emerging Economies (CEADs, 2023). Table 2 displays descriptive statistics for all variables at the level of provinces and municipalities from 2005 to 2019. To convert the STIRPAT model into a standard linear model, a key step in our empirical analysis is the logarithmic transformation of all variables. This allows for a more precise description and analysis of the data, aiding in a better understanding of the dynamic relationship between industrial structure and carbon emission intensity across different regions in China.
4. Results and discussion
4.1. Global autocorrelation analysis of carbon emission intensity
In this study, Moran's I statistics was utilized to assess the global spatial autocorrelation of carbon emission intensity in different regions in China from 2005 to 2019. The specific results of this analysis, as presented in Table 3, strongly confirm the significant existence of spatial autocorrelation and spatial spillover effects in carbon emission intensity at the regional level in China during the period from 2005 to 2018.
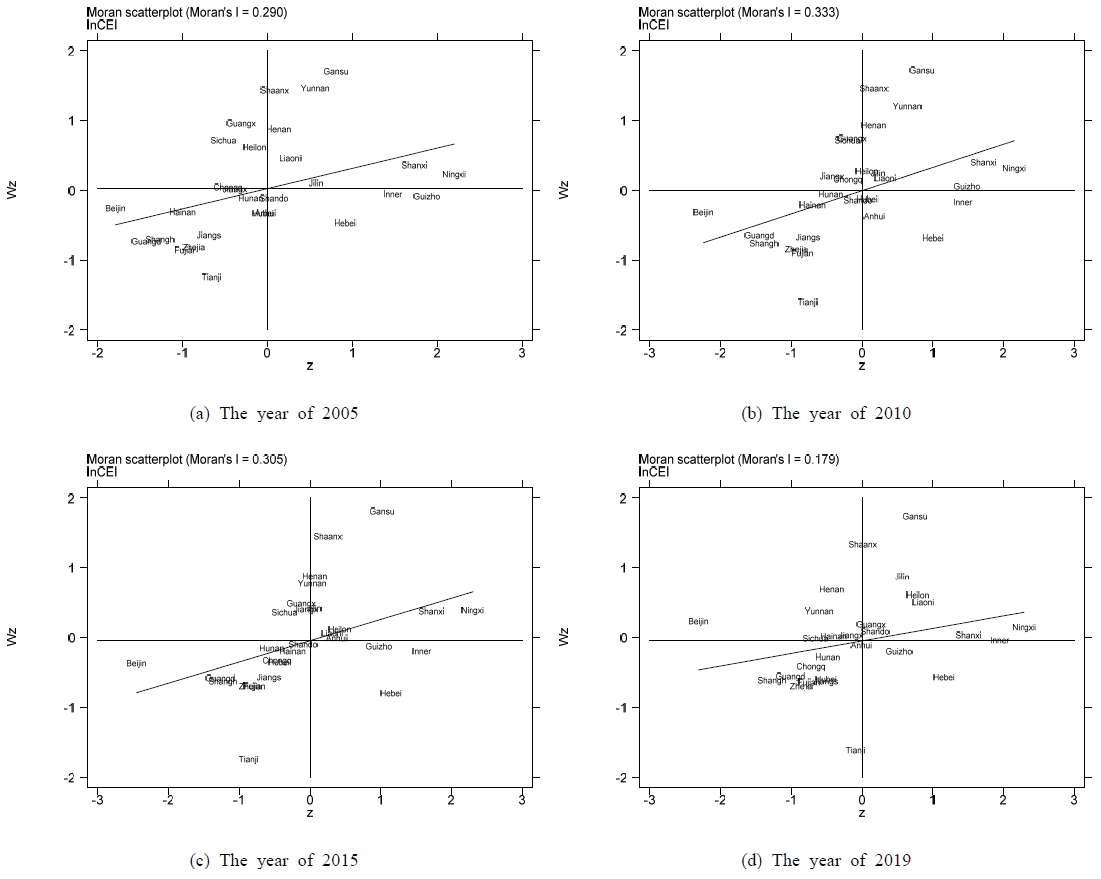
This study calculates the local Moran's I index of carbon emission intensity across China for the years from 2005 to 2019, with particular emphasis on 2005, 2010, 2015, and 2019. Using the local Moran's I scatter plot quadrants, we classify carbon emission intensity into four different clustering types for different Chinese regions. Fig. 1 shows these classifications, which effectively highlight the spatial patterns and regional differences in carbon emission intensity during these key years.
The four Moran scatterplots in Fig. 1 show that, over the years 2005, 2010, 2015, and 2019, Chinese regions exhibit four types of carbon emission intensity clustering: high-high, low-low, high-low, and low-high4). Northern and central-western China are characterised by high-high clusters, which are rich in natural resources but underdeveloped economically. Reliance on energy-intensive industries, coupled with a lack of advanced sectors, leads to poor resource efficiency and high emissions. In contrast, the coastal regions, which fall into the low-low clusters, demonstrate economic advancement with technology-rich industries, fostering high energy efficiency and lower emissions. Provinces such as Inner Mongolia, Guizhou, and Hebei are high-low clusters. Despite their high emissions, these provinces have a minimal impact on the emissions of their neighbors. This study reveals a strong spatial correlation in the carbon emission intensity of China’s provinces, highliting distinct regional disparities and trends.
4.2. Basic regression results
The Hausman test indicates that a fixed-effects model is more appropriate for our analysis than a random-effects model. Consequently, we employ the two-way fixed effects model, and the estimated results are shown in Table 4. Simultaneously, we also categorized the samples into eastern, middle, and western regions based on traditional Chinese regional divisions. This classification allows for a nuanced analysis of how the development of digital industry affects carbon emission intensity in different regions of China. A detailed breakdown of the regional divisions is shown in Fig. 2.
For the full sample and the central and western regional subsamples, we observed a significant negative correlation betweenthe the a the digital industry development and carbon emission intensity. For example, the estimated coefficient implies that a 10% increase in the proportion of income from digital industry in GDP is associated with 0.32% decrease in carbon emission intensity. This suggests that advances in digital industry lead to significant reductions in emissions, highlighting the importance of digitalization in reducing carbon emissions, especially in these areas.
4.3. Statistical test results
Before inferring with the Spatial Durbin Model (SDM), we first employed statistical testing methods such as the Lagrange Multiplier (LM), Likelihood Ratio (LR), and Hausman tests. The constructed Moran's I statistic in Table 5, derived from our model's residuals, tests for spatial autocorrelation in the OLS model residuals, indicating if the spatial model captures spatial dependencies. A significant deviation from zero highlights the need for spatial econometric models. According to the results in Table 5, most LM tests rejected the null hypothesis, indicating the presence of SAR and SEM elements, further supporting the SDM. The LR test rejected the null hypothesis of simplifying the SDM to SAR or SEM, solidifying the SDM's position as the preferred model. Lastly, the Hausman test results endorsed the use of the bidirectional fixed effects SDM for comprehensive spatial econometric analysis.
4.4. Empirical results of the Spatial Durbin model
This study evaluated spatial models using a geo-economic nested matrix. The two-way Fixed Effects Spatial Durbin model was found to be the most appropriate for the sample data. The spatial regression analysis in Table 6 shows an effective model simulation with significant spatial autocorrelation at the 1% level, suggesting spatial spillovers in carbon emission intensity across provinces and cities. The development of the digital industry shows a significant negative effect on carbon emission intensity at the 1% level, consistent with Yang et al. (2023). This industry, which is characterized by high value-added and environmentally friendly features, can reduce fossil fuel consumption and carbon emissions. Technological and economic spillovers from the digital industry further help to reduce carbon emissions.
The Spatial Durbin Model elucidates the multidimensional impact of digital industry development on carbon emission intensity through direct, indirect, and total effects, as shown in Table 6. Direct effects show how digital industry growth affects carbon emission intensity within the same region, while indirect effects explore its influence on the carbon emission intensity of neighboring regions. Despite the substantial reduction in carbon emission intensity attributed to digital industry development, as evidenced by significant direct and total effects, the spatial spillover effect remains insignificant, indicating a limited diffusion of benefits across provinces.
Digital technologies contribute to reducing carbon emission intensity by enhancing energy efficiency, reducing energy consumption per unit of output, and facilitating the optimization of industrial structure. However, the spatial spillover of these benefits is limited, possibly due to the challenges that neighboring areas face in adopting green technologies and management practices. Differences in regional levels of development, technological advancements and policy frameworks further hinder the spatial diffusion of these effects. Although the indirect effect is not significant, the contribution of the digital economy to reducing carbon emission intensity is profound, underlining its pivotal role in reducing overall carbon emissions.
In our study, we found that the level of economic development is significantly negatively correlated with carbon emission intensity at the 1% confidence level, accompanied by a strong spatial spillover effects. In addition, the population structure (proportion of the working population and population aging) is significantly positively correlated with carbon emission intensity, also significant spatial spillover effects. Foreign trade has a significant positive effect on carbon emissions, implying that increased trade increases local and regional emissions in China. Interestingly, R&D investment has a statistically positive relationship with emissions in our study, contrary to the expectation of green development. When controlling for the degree of digital industry development and industrial structure, regional R&D investment is linked to higher emission intensity. This may reflect a regional focus on boosting production and economic growth without prioritizing low-carbon principles.
While the direct effects of industrial structure and urbanization rate are not significant, their spillover effects are significantly negative. This is consistent with Luo et al. (2023), which suggests a complex, non-linear relationship between these factors and carbon emissions.
5. Conclusions
This study builds on existing research to deepen our understanding of the impact of digital industrialization on carbon emission intensity. We use provincial panel data from 2005 to 2019 to conduct empirical analysis employing the two-way Fixed Effects Model and the two-way Fixed Effects Spatial Durbin Model. This approach allows us to examine the impact of digital economy on carbon emission intensity, both within and across different regions.
From the empirical results, we find that China's digital industry advancement could potentially reduce carbon emission intensity. However, this effect varies regionally, with a stronger impact in the central and eastern regions compared to the less developed western areas. From a spatial perspective, the growth of digital industry contributes to local and overall carbon reduction. However, the results indicate that the spatial spillover effect among provinces remains limited.
This study's findings lead to several policy recommendations to support China's “3060 dual carbon goals” and sustainable economic development. Firstly, there is a pressing need to encourage comprehensive digital transformation in traditional industries. Such transformation is essential for promoting green, low-carbon transitions, especially by investing in digital industry technologies that foster green development and focusing on innovations that directly reduce carbon emissions in sectors with high carbon reduction potential. Secondly, our analysis highlights the importance of accelerating the green energy transformation. This can be achieved by transforming key carbon-emitting sectors through increasing the use of non-fossil energy sources and improving energy efficiency. The integration of digital technologies is crucial in driving innovation within the energy sector, thereby enhancing the efficiency of energy use and establishing a new paradigm for clean, efficient, and low-carbon energy systems. Lastly, to address the association between carbon emissions and demographic factors such as labor force size and population aging, it is recommended to promote green household energy practices. This approach aims to mitigate the environmental impacts associated with demographic changes and places an emphasis on energy conservation and efficiency at the household level.
This paper primarily examines the impact of the digital industry development on regional carbon emissions. As digitalization progresses and the digital economy advances, future research may focus on the underlying mechanisms how and why digital industry are associated with carbon emissions reductions. Understanding consumer behavior in the digital age and its contribution to carbon emissions could be another critical area. This includes studying the environmental impact of consumer-driven digital trends like online streaming and shopping. Future research in these areas will enhance our understanding of the green impacts of digitalization, informing policy-making as well as contributing to a more sustainable future.
Acknowledgments
This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2023S1A5A2A21085534). Also, this work was supported by the Pukyong National University Research Fund in 2021 (CD20210988).
Notes
References
-
Adedoyin FF, Alola AA, Bekun FV. 2020. An assessment of environmental sustainability corridor: The role of economic expansion and research and development in EU countries. Sci Total Environ 713: 136726.
[https://doi.org/10.1016/j.scitotenv.2020.136726]

-
Ali HS, Abdul-Rahim AS, Ribadu MB. 2017. Urbanization and carbon dioxide emissions in Singapore: Evidence from the ARDL approach. Environ Sci Pollut Res 24(2):1967-1974.
[https://doi.org/10.1007/s11356-016-7935-z]

-
Ali R, Bakhsh K, Yasin MA. 2019. Impact of urbanization on CO2 emissions in emerging economy: Evidence from Pakistan. Sustain Cities Soc 48:101553.
[https://doi.org/10.1016/j.scs.2019.101553]

-
Anser MK. 2019. Impact of energy consumption and human activities on carbon emissions in Pakistan: Application of STIRPAT model. Environ Sci Pollut Res 26(13): 13453-13463.
[https://doi.org/10.1007/s11356-019-04859-y]

- BP. 2023. Statistical review of world energy; [accessed 2023 Nov 6]. https://www.bp.com/en/global/corporate/energy-economics
- CDEDR (China Digital Economy Development Report). 2023. http://www.caict.ac.cn/english/research/whitepapers/202311/P020231101476013122093.pdf
- CEADs (Carbon Emission Accounts and Datasets for Emerging Economies). 2023. CEADs Data; [accessed 2023 Nov 13]. https://www.ceads.net/
-
Cheng Z, Li L, Liu J. 2018. Industrial structure, technical progress and carbon intensity in China's provinces. Renew Sustain Energy Rev 81(Part 2): 2935-2946.
[https://doi.org/10.1016/j.rser.2017.06.103]

-
Dong F, Long R, Li Z, Dai Y. 2016. Analysis of carbon emission intensity, urbanization and energy mix: Evidence from China. Nat Hazards 82(2): 1375-1391.
[https://doi.org/10.1007/s11069-016-2248-6]

-
Ge LY, Mo LJ, Huang NB. 2022. Development of digital economy: Upgrading of industrial structureand urban carbon emission (in Chinese with English abstract). Mod Financ Econ J Tianjin Univ Finan Econ 42(10): 20-37.
[https://doi.org/10.19559/j.cnki.12-1387.2022.10.002]

-
Golgher AB, Voss PR. 2016. How to interpret the coefficients of spatial models: Spillovers, direct and indirect effects. Spat Demogr 4: 175-205.
[https://doi.org/10.1007/s40980-015-0016-y]

-
Guo X, Ren D, Shi J. 2016. Carbon emissions, logistics volume and GDP in China: Empirical analysis based on panel data model. Environ Sci Pollut Res 23(24): 24758-24767.
[https://doi.org/10.1007/s11356-016-7615-z]

-
Huang J, Liu Q, Cai X, Hao Y, Lei H. 2018. The effect of technological factors on China's carbon intensity: New evidence from a panel threshold model. Energy Policy 115: 32-42.
[https://doi.org/10.1016/j.enpol.2017.12.008]

-
Hwang JH, Choi YY, Yoo YJ, Sun ZM, Cho HJ, Jeon SW. 2021. Analysis of land use changes and carbon storage by region under the Seoul metropolitan area: Readjustment planning act using the InVEST carbon model (in Korean with English abstract). J Clim Chan Res 12(5-1): 523-535.
[https://doi.org/10.15531/KSCCR.2021.12.5.523]

-
Jiang JH. 2021. Sustainable digital era: High-quality integrated development of green economy and digital economy (in Chinese with English abstract). Enterp Econ 7: 23-30.
[https://doi.org/10.13529/j.cnki.enterprise.economy.2021.07.003]

-
Ki HC, Seong MY. 2023. Analysis on the efficiency of the Korean carbon emissions market: comparison with the European emissions mark. Journal of The Korean Data Analysis Society. 25(1):235-247. (in Korean with English abstract).
[https://doi.org/10.37727/jkdas.2022.25.1.235]

-
Kim GW, Noh DW, Lee JW. 2019. Estimating greenhouse gas emission efficiency of firms in South Korea: A stochastic frontier analysis approach (in Korean with English abstract). J Clim Chang Res 10(2): 117-128.
[https://doi.org/10.15531/KSCCR.2019.10.2.117]

- Li MY, Sun LY. 2022. Research on paths of information and communication industry achieving carbon peaking and carbon neutrality goals. Inf Commun Technol 90(4): 43-48.
-
Liu LC, Wu G, Wang JN, Wei YM. 2011. China’s carbon emissions from urban and rural households during 1992-2007. J Clean Prod 19(15): 1754-1762.
[https://doi.org/10.1016/j.jclepro.2011.06.011]

-
Luo ZX, Zhao YW, Lim JM. 2023. The nonlinear effect of population aging and socio-economic conditions on carbon emission: An empirical analysis of 30 provinces and regions in China. J Korean Data Anal Soc 25(3): 883-902.
[https://doi.org/10.37727/jkdas.2023.25.3.883]

-
Moran PAP. 1950. Notes on continuous stochastic phenomena. Biometrika 37(1/2): 17-23.
[https://doi.org/10.2307/2332142]

- NBS (National Bureau of Statistics of China). 2023. NBS national data; [accessed 2023 Nov 20]. http://www.stats.gov.cn/
-
Xie YF. 2022. The effect and mechanism of digital economy on regional carbon emission intensity. Contemp Econ Manag 44(2): 68-78.
[https://doi.org/10.13253/j.cnki.ddjjgl.2022.02.008]

-
Yang GQ, Wang HS, Fan HS, Yue ZY. 2023. Carbon reduction effect of digital economy: Theoretical analysis and empirical evidence (in Chinese with English abstract). China Ind Econ 5: 80-98.
[https://doi.org/10.19581/j.cnki.ciejournal.2023.05.005]

-
Zhang N, Yu K, Chen Z. 2017. How does urbanization affect carbon dioxide emissions? A cross-country panel data analysis. Energy Policy 107: 678-687.
[https://doi.org/10.1016/j.enpol.2017.03.072]

- Zhang W, Hu Y. 2020. The effect of innovative human capital on green total factor productivity in the Yangtze River Delta (in Chinese with English abstract). China Popul Resour Environ 30(9): 106-120.
-
Zhou Y, Poon J, Yang Y. 2021. China's CO2 emission intensity and its drivers: An evolutionary Geo-Tree approach. Resour Conserv Recycl 171: 105630.
[https://doi.org/10.1016/j.resconrec.2021.105630]